Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin. -- John von Neumann
Computers are terrible at generating randomness, and aside from hardware assisted methods there is no way to obtain true randomness. Instead there has been a considerable research into the development of Pseudorandom Number Generators.
The best way to visualize a Pseudorandom Number Generator is as a deck of cards.
The step where you shuffle the deck is called seeding. The number of cards in your deck is called the period. Since computers are bad at "random" (since they are by nature, deterministic), over the years people have come up with various mathematical formula that attempt to produce sequences of numbers that resemble random data.
It is worthwhile to note that the vast majority of video games use a PRNG of some sort. The notable exceptions would be the online gambling establishments which use hardware RNGs.
Note: This is accurate to the best of my knowledge as of the 2012/10/11 patch. The fact that the game saves/restores the PRNG state is irrelevant to this analysis.
Using a UnrealScript decompiler, it's possible to look at how the tactical game calculates if a shot hit or not.
From XGAction_Fire:
function CalcHitRolls()
{
local XGUnit TargetUnit;
local int iNewHP;
// End:0x4d Loop:False
if(m_kShot.GetType() == 78)
{
m_bKillShot = false;
m_bHit = false;
m_bCritical = false;
}
// End:0xcc
else
{
m_bKillShot = false;
m_kShot.RollForHit();
m_bHit = m_kShot.IsHit();
m_bCritical = m_kShot.IsCritical();
}
m_bReflected = m_kShot.IsReflected();
m_iDamage = m_kShot.GetActualDamage();
Each time you take a shot, the game calls m_kShot.IsHit(). This routine is abstracted, away but what it ends up doing eventually is to call into the native executable itself.
From XGAbility_Targeted:RollForHit():
m_bHit = XComGameReplicationInfo(class'Engine'.static.GetCurrentWorldInfo().GRI).m_kGameCore.RollForHit(fChance, m_kUnit.GetCharacter().m_kChar, GetPrimaryTarget().GetCharacter().m_kChar, fRoll);
The actual native code glue routine looks like this:
function bool RollForHit(float fChance, out TCharacter kShooter, out TCharacter kTarget, out float fRoll)
{
fRoll = class'XComEngine'.static.SyncFRand(string(Name) @ string(GetStateName()) @ string(GetFuncName()));
return fRoll <= fChance;
}
SyncFRand returns a floating point number between 0.0 and 1.0. If your chance to hit is greater than or equal to what the PRNG rolls, you hit. This is done per shot you take, as would be expected.
Using a disassembler, it's possible to look at what PRNG XCOM: EU uses, and how it calculates it's seed.
The UnrealScript to native binding is in the form of a simple table in the executable with method names followed by function addresses.
.data:01D00B70 dd offset aUxcomengine_17 ; "UXComEngineexecGetARandomSeed"
.data:01D00B74 dd offset sub_A76810
.data:01D00B78 dd offset aUxcomengine_18 ; "UXComEngineexecSyncVRand"
.data:01D00B7C dd offset sub_88F2F0
.data:01D00B80 dd offset aUxcomengine_19 ; "UXComEngineexecSyncFRand"
.data:01D00B84 dd offset sub_109D9E0
.data:01D00B88 dd offset aUxcomengine_20 ; "UXComEngineexecSyncRand"
.data:01D00B8C dd offset sub_D40F90
.data:01D00B90 dd offset aUxcomengine_21 ; "UXComEngineexecGetSyncSeed"
.data:01D00B94 dd offset sub_5493F0
.data:01D00B98 dd offset aUxcomengine_22 ; "UXComEngineexecSetRandomSeeds"
.data:01D00B9C dd offset sub_8ED430
Seed generation is done in UXComEngineexecGetARandomSeed:
.text:00A76844 call ds:QueryPerformanceCounter
.text:00A7684A mov ecx, [esp+8+arg_4]
.text:00A7684E mov edx, [esp+8+var_8]
.text:00A76851 mov [ecx], edx
.text:00A76853 add esp, 8
.text:00A76856 retn 8
QueryPerformanceCounter is a Windows library call that wraps the RDTSC instruction which returns the number of ticks since the system was powered up.
As far as methods for generating the initial seed goes, this is common and acceptable since it's reasonable to expect that it will be unpredictable each time it's called.
The actual PRNG is common code between UXComEngineexecSyncVRand, UXComEngineexecSyncFRand and UXComEngineexecSyncRand:
.text:00AE6B10 sub_AE6B10 proc near ; CODE XREF: sub_523E50+6Ep
.text:00AE6B10 ; sub_880680+13p ...
[stuff irrelevant to the PRNG omitted]
.text:00AE6B65 mov eax, [esi+834h]
.text:00AE6B6B imul eax, 0BB38435h
.text:00AE6B71 add eax, 3619636Bh
.text:00AE6B76 mov [esi+834h], eax
.text:00AE6B7C add esp, 14h
.text:00AE6B7F and eax, 7FFFFFh
.text:00AE6B84 or eax, 3F800000h
.text:00AE6B89 mov [esp+0Ch+arg_0], eax
.text:00AE6B8D movss xmm0, [esp+0Ch+arg_0]
.text:00AE6B93 cvttss2si edx, xmm0
.text:00AE6B97 mov [esp+0Ch+var_4], edx
.text:00AE6B9B fild [esp+0Ch+var_4]
.text:00AE6B9F pop edi
.text:00AE6BA0 pop esi
.text:00AE6BA1 fsubr [esp+4+arg_0]
.text:00AE6BA5 pop ecx
.text:00AE6BA6 retn 4
Since x86 assembly language isn't everyone's cup of tea, this is the same algorithm expressed in C:
uint32_t seed; /* Set elsewhere. Actually contained in an C++ object (esi + 0x834) */
float random_number_plox() {
static union {
uint32_t i;
float f;
} foo;
int bar;
/* LCG: x = 0x0BB38435 * x' + 0x3619636B */
foo.i = seed * 0x0BB38435;
foo.i += 0x3619636B;
seed = foo.i;
/* Convert the integer to a floating point number between 1.0 and 2.0 by
* manipulating the floating point format.
*/
foo.i = foo.i & 0x7FFFFF | 0x3F800000;
return foo.f - 1.0f; /* Return something between 0.0 and 1.0 */
}
The PRNG used is a Linear Congruential Generator with a = 0x0BB38435, and c = 0x3619636. It is worth noting that this is the same LCG that is used in the RFC 6716 Opus Audio Codec.
Given the nature of the algorithm, running any in-depth battery of tests against it is sort of a futile gesture. By the nature of the algorithm it uses, any stringent test suite will expose the fact that the LCGs just aren't that great.
Sample dieharder output:
#=============================================================================#
# dieharder version 3.31.1 Copyright 2003 Robert G. Brown #
#=============================================================================#
rng_name |rands/second| Seed |
stdin_input_raw| 4.95e+06 |3116752171|
#=============================================================================#
test_name |ntup| tsamples |psamples| p-value |Assessment
#=============================================================================#
diehard_birthdays| 0| 100| 100|0.85423762| PASSED
diehard_operm5| 0| 1000000| 100|0.57756795| PASSED
diehard_rank_32x32| 0| 40000| 100|0.44242249| PASSED
diehard_rank_6x8| 0| 100000| 100|0.00000000| FAILED
diehard_bitstream| 0| 2097152| 100|0.00000000| FAILED
diehard_opso| 0| 2097152| 100|0.00000000| FAILED
diehard_oqso| 0| 2097152| 100|0.00000000| FAILED
diehard_dna| 0| 2097152| 100|0.00000000| FAILED
diehard_count_1s_str| 0| 256000| 100|0.00000000| FAILED
diehard_count_1s_byt| 0| 256000| 100|0.00000000| FAILED
diehard_parking_lot| 0| 12000| 100|0.24520972| PASSED
diehard_2dsphere| 2| 8000| 100|0.78720303| PASSED
diehard_3dsphere| 3| 4000| 100|0.15511214| PASSED
diehard_squeeze| 0| 100000| 100|0.28686614| PASSED
diehard_sums| 0| 100| 100|0.15599805| PASSED
diehard_runs| 0| 100000| 100|0.41809458| PASSED
diehard_runs| 0| 100000| 100|0.02141932| PASSED
diehard_craps| 0| 200000| 100|0.27456230| PASSED
diehard_craps| 0| 200000| 100|0.53873948| PASSED
[Further results omitted]
Note: The OPSO, OQSO and DNA tests are tagged by the suite maintainer as "Suspect" reliability, and the sums test is tagged as "Do Not Use". It's also important to have multiple runs, and examine the p-values for the tests that pass, so the results posted should not be taken as anything more than an example.
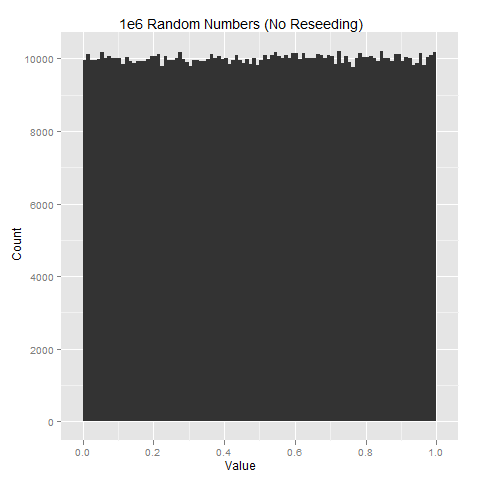
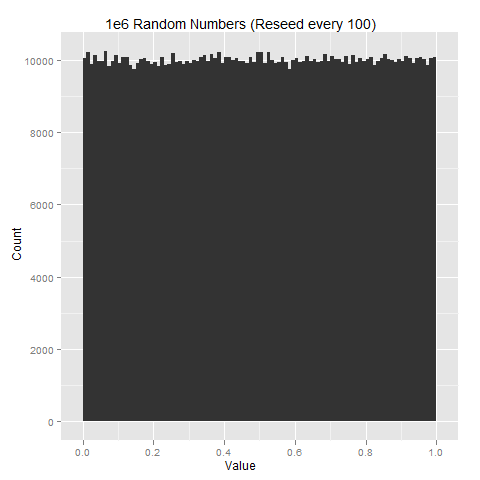
A computer may be able to find correlations between the output, because they are considerably better than humans are at pattern matching, but unless the bias is blatantly obvious, it is unlikely that a human can. To examine this, 1 million random numbers were generated and simple histogram plots were constructed.


As a comparison, this what the non-reseeding case will look like with a modern PRNG (WELL512a) that passes most statistical tests
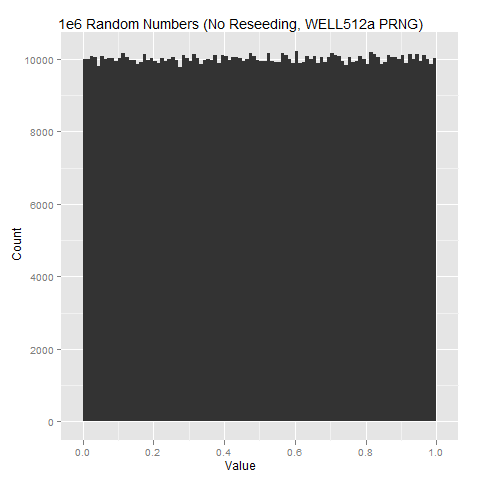
To the casual observer there should not be much difference between the histogram plot from the XCOM: EU PRNG and the one generated using a modern high quality PRNG.
There naturally are flaws with the algorithm, and it is not what I would recommend as a first choice for this sort of application. This comes in two forms.
The first is that due to using m that is a power of 2, the entropy in the low bits of the output is rather limited. This results in less entropy in the lower bits of the mantissa, but it doesn't appear to affect the equidistribution or streakiness of the output.
The second major algorithm defect is in the form of serial correlation. It is the author's opinion that this is a non-issue for the average end user as it takes a massive sample size to be able to detect this in the output assuming one is working directly off the PRNG output. Given that the acutal output is opaque, it is extremely unlikely that this will be noticable over the course of a playthrough. Additionally the bias affects rolls made by both sides, thus the actual impact on fairness should be negligible.
The tactical portion of the game does what is expected, correctly. The method the game uses for seed generation is fine. The underlying PRNG is not great and could be replaced, but the deficiencies in the algorithm should have minimal impact on game play. When you miss 3 90% shots in a row, you just got unlucky, the game is not cheating you out of your kills.
For a different approach to examining fairness and a excellent look into how to examine this kind of problem without resorting to reverse engineering, John Mount's "Win-Vector Blog: How to test XCOM 'dice rolls' for fairness" is strongly recommended as further reading (statistical tests on serial correlation also examined in the comments).
The (rather messy) C source code that I used to generate the data for the graphs is available on request.
The XCOM:EU PRNG as a R routine is available here for those that wish to use it as a basis for futher statistical analysis.